 Impedansi listrik, atau lebih sering disebut impedansi,
menjelaskan ukuran penolakan terhadap arus bolak-balik sinusoid.
Impedansi listrik memperluas konsep resistansi listrik ke sirkuit AC,
menjelaskan tidak hanya amplitudo relatif dari tegangan dan arus, tetapi
juga fase relatif. Impedansi adalah kuantitas kompleks yang dinotasikan
dengan
Impedansi listrik, atau lebih sering disebut impedansi,
menjelaskan ukuran penolakan terhadap arus bolak-balik sinusoid.
Impedansi listrik memperluas konsep resistansi listrik ke sirkuit AC,
menjelaskan tidak hanya amplitudo relatif dari tegangan dan arus, tetapi
juga fase relatif. Impedansi adalah kuantitas kompleks yang dinotasikan
dengan dan istilah impedansi kompleks mungkin dapat dipertukarkan. Bentuk kutub secara praktis menunjukkan baik karakteristik magnitudo dan fase,
dan istilah impedansi kompleks mungkin dapat dipertukarkan. Bentuk kutub secara praktis menunjukkan baik karakteristik magnitudo dan fase, menunjukkan perbandingan amplitudo perbedaan tegangan terhadap amplitudo arus,
menunjukkan perbandingan amplitudo perbedaan tegangan terhadap amplitudo arus,  memberikan perbedaan fase antara tegangan dan arus, sedangkan
memberikan perbedaan fase antara tegangan dan arus, sedangkan  adalah bilangan imajiner.
adalah bilangan imajiner.Dalam koordinat kartesius,
 dan bagian imajiner adalah reaktansi
dan bagian imajiner adalah reaktansi  . Secara dimensi, impedansi sama dengan resistansi; dan satuan SI adalah ohm. Istilah impedansi digunakan pertama kali oleh Oliver Heaviside pada Juli 1886. Arthur Kennelly adalah yang pertama kali menunjukkan impedansi dengan bilangan kompleks pada 1893. Kebalikan dari impedansi adalah admitansi.
. Secara dimensi, impedansi sama dengan resistansi; dan satuan SI adalah ohm. Istilah impedansi digunakan pertama kali oleh Oliver Heaviside pada Juli 1886. Arthur Kennelly adalah yang pertama kali menunjukkan impedansi dengan bilangan kompleks pada 1893. Kebalikan dari impedansi adalah admitansi.HUKUM OHM
 Maksud dari impedansi listrik dapat dimengerti dengan mensubtitusikan ke hukum Ohm.
Maksud dari impedansi listrik dapat dimengerti dengan mensubtitusikan ke hukum Ohm. berperan seperti resistansi, memberikan penurunan tegangan membentangi impedansi
berperan seperti resistansi, memberikan penurunan tegangan membentangi impedansi  untuk arus yang diberikan
untuk arus yang diberikan  . Faktor fase menjelaskan bahwa arus tertinggal dari tegangan dengan fase
. Faktor fase menjelaskan bahwa arus tertinggal dari tegangan dengan fase  (pada domain waktu, isyarat arus digeser
(pada domain waktu, isyarat arus digeser  kesebelah kiri isyarat tegangan).
kesebelah kiri isyarat tegangan).Karena impedansi memperluas hukum Ohm untuk mencakup sirkuit AC, hasil dari analisis sirkuit DC seperti pembagian tegangan, pembagian arus, teorema Thevenin dan teorema Norton, dapat juga diperluas ke sirkuit AC dengan mengganti resistansi dengan impedansi.
TEGANGAN DAN ARUS KOMPLEKS
 Untuk mempermudah perhitungan, gelombang tegangan dan arus sinusoidal
biasanya digambarkan sebagai fungsi nilai-kompleks dari waktu diartikan
sebagai
Untuk mempermudah perhitungan, gelombang tegangan dan arus sinusoidal
biasanya digambarkan sebagai fungsi nilai-kompleks dari waktu diartikan
sebagai  dan
dan  .
.Validitas perwakilan kompleks
Perwakilan ini menggunakan eksponensial kompleks dapat dibuktikan dengan rumus Euler:Fasor
Fasor adalah bilangan kompleks yang tetap, biasanya dinyatakan dalam bentuk eksponensial, mewakili amplitudo kompleks (magnitudo dan fase) dari fungsi sinusoid dari waktu. Fasor digunakan oleh ahli elektronik untuk mempermudah perhitungan yang melibatkan sinusoid, dimana persamaan diferensial dapat diubah ke aljabar.Impedansi dari unsur sirkuit dapat didefinisikan sebagai perbandingan tegangan fasor yang membentangi unsur dengan arus fasor yang mengaliri unsur, seperti yang ditetapkan oleh amplitudo relatif serta fase dari tegangan dan arus. Ini identik dengan definisi dari hukum Ohm diatas, mengakui bahwa faktor
 saling meniadakan.
saling meniadakan.






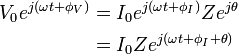


![\cos(\omega t+\phi)=\frac{1}{2}\Big[e^{j(\omega t+\phi)}+e^{-j(\omega t+\phi)}\Big]](http://upload.wikimedia.org/math/5/0/0/5009e7426179d0228b263b82c81f9dac.png)

Tidak ada komentar :
Posting Komentar